
嶽麓書院藏秦簡《數》贏不足算題研討
(首發)
蕭燦
湖南大學嶽麓書院
嶽麓書院藏秦簡《數》中有一例“贏不足”算題非常重要,它是一例含三個未知數的不定問題,不見於傳世文獻和已知的出土文獻。對於此題學者們有各種解讀,但簡所記術文的含義仍無法確知🔲。
![]() 斗九錢,秶十
斗九錢,秶十 ![]() C020107
C020107
![]() 七錢🧶👨🏼🦰,叔(菽)十斗
七錢🧶👨🏼🦰,叔(菽)十斗![]() 2197
2197
![]() 斗👨🏼✈️,用八錢🛬,問各幾可(何)🏇🏿?曰🧑🏼🚒:稻六斗 0799
斗👨🏼✈️,用八錢🛬,問各幾可(何)🏇🏿?曰🧑🏼🚒:稻六斗 0799
![]() 〔術〕曰:直(置)稻九,不足一其下🍧,粢七,直(置)贏
〔術〕曰:直(置)稻九,不足一其下🍧,粢七,直(置)贏 ![]() 2198
2198
![]() 一其下,叔(菽)五,直(置)贏三其下,粢不足
一其下,叔(菽)五,直(置)贏三其下,粢不足 ![]() 2179
2179
![]() 乘粢七,同之卅,為稻
乘粢七,同之卅,為稻![]() (實);以叔(菽)三乘叔(菽)五,十五為粢
(實);以叔(菽)三乘叔(菽)五,十五為粢![]() (實)🫷🏿,以稻不足一乘叔(菽)五為
(實)🫷🏿,以稻不足一乘叔(菽)五為![]() (實),同贏 0496
(實),同贏 0496
![]() 不足 C100108
不足 C100108
![]() 五以為法,如法各得一斗🚨。 0497
五以為法,如法各得一斗🚨。 0497
簡文的復原方案之一可以是⇢:“【稻十】斗九錢🧝🏿♂️,秶十【斗】七錢,叔(菽)十斗【五錢,今欲買三物共十】斗,用八錢,問各幾可(何)🏋🏽♂️?曰:稻六斗🌬,【秶三斗⬇️,菽一斗🎼😳。術】曰:置稻九,不足一其下,粢七🤹🏻,直(置)贏一其下👩🏼✈️,叔(菽)五,直(置)贏三其下,粢不足【一乘稻九🧑🏼🤝🧑🏼,以叔(菽)三】乘粢七,同之卅🕴🏼,為稻實;以叔(菽)三乘叔(菽)五,十五為粢![]() (實);以稻不足一乘叔(菽)五為
(實);以稻不足一乘叔(菽)五為![]() (實),同贏、不足五以為法,如法各得一斗👩🏻🏫。”[1]
(實),同贏、不足五以為法,如法各得一斗👩🏻🏫。”[1]
徐義保先生的解析[2]
此題的代數方法的解答如下𓀙:
設稻![]() 斗,秶為
斗,秶為![]() 斗,菽
斗,菽![]() 斗🏌🏽♂️🚴🏻,列方程組🆑🛹:
斗🏌🏽♂️🚴🏻,列方程組🆑🛹:
![]()
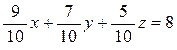
這一不定方程組有無數解👰🏼,如:
![]()
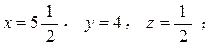
算題給出的答案![]() 只是其中之一。
只是其中之一。
依照算題術文,布列如下:
稻 9 1(不足)
秶 7 1(贏)
菽 5 3(贏)
![]()
![]()
![]()
上述運算步驟,數據于算題術文吻合,但不能解釋其數學含義。
鄒大海先生的解析[3]
此題的代數方法解答如下:
設稻![]() 斗,秶為
斗,秶為![]() 斗🧎🏻♂️➡️,菽
斗🧎🏻♂️➡️,菽![]() 斗,列方程組👝🛄:
斗,列方程組👝🛄:
x+y+z=10 (1)
9x/10+7y/10+5z/10=8 (2)
綜合兩式得到2x+y=15,如果求非負整數解,
當y=1時,x=7,z=2🏇🏼,這組解可計為(7,1,2)🚇, 第一組
當y=3時,這組解為(6🧜🏿🧛🏿,3✮,1), 第二組
當y=5時,這組解為(5,5,0), 第三組
當y=7或9或更大的奇數時,z為負數,故不可計入解。
本題的答案中說“稻六斗”,可見只取了第二組解💶。
依照算題術文,可作如下理解🙋🏼👩🏿🍼:
|
直(置) |
稻 九 |
秶 七 |
叔 五 |
|
|
不足 一 |
贏 一 |
贏 三 |
秶1×稻9+叔(菽)3×秶7=30 為稻實
叔(菽)3×叔(菽)5 =15 為秶實
稻不足1×叔(菽)5=5 為叔實
贏1+贏3+不足1=5 為法
以法5分別除稻實30、秶實15🌴、叔實5🤱🏼,分別得到稻🛞、秶、叔的數量為6、35️⃣💂🏿♂️、1斗。
上述各實的計算步驟,沒有規則可言,整個計算也看不出有什麼道理🚙。古人在設計這個問題的時候,可能就是先有答案和題設🏌🏼♂️,然後擬合術文的。
朱一文先生的意見[4]
朱先生同意徐、鄒二位先生對算法的分析,但認為簡所記術文並非拼湊擬合,而是體現的算籌運算的規律。簡文的“術”或者在某些限制條件下是成立的。
[1] 此復原方案參考了鄒大海先生的意見。鄒大海先生現為中科院自然科學史研究所研究員🚣🏿♂️。
![]() (實),從“宀”從“貫”。在《數》中“實”字多數情況下寫為“
(實),從“宀”從“貫”。在《數》中“實”字多數情況下寫為“![]() ”,也有幾處寫為“
”,也有幾處寫為“![]() ”,這是省去了“宀”,將“毌”寫作“尹”或者“君”🍙。
”,這是省去了“宀”,將“毌”寫作“尹”或者“君”🍙。
[2] 引自徐義保先生的電子郵件🚼,2010-10-24。徐義保先生現為美國紐約城市大學副教授。
[3] 引自鄒大海先生的電子郵件👴🏼,2010-11-2。
[4] 引自在中科院自然科學史研究所的談話,2011-4-7🎳。朱一文先生現為該研究所博士🧛🏼♀️。
本文收稿日期為2011年4月12日👩🏻🦽➡️。
本文發佈日期為2011年4月12日🧑✈️。
点击下载附件🦞: 0839蕭燦:嶽麓書院藏秦簡《數》贏不足算題研討
0839蕭燦:嶽麓書院藏秦簡《數》贏不足算題研討
Copyright 富达平台 - 注册即送,豪礼相随!版权所有 沪ICP备10084952号 地址:富达注册光华楼西主楼27楼 邮编:200433
感谢上海屹超信息技术有限公司提供技术支持
總訪問量:737967